GEODESICS ON MESHES

Measuring geodesic distances and the computation of paths on a mesh is widely used in computational geometry for many different applications ranging from mesh parameterization and remeshing to skinning and mesh deformation. After a longer conversation and chat about this topic, and since i thought it could be useful at some point I finally got my feet wet on different algorithms to compute such geodesics in Houdini.
The first and obvious choice was to compute the shortest path between the source point and all the other points on the geometry. This was easy and fast to do but unfortunately it doesn’t compute geodesics. Since the underlying algorithm of the ShortestPathSop (Dijkstra) relies on the edges of the mesh, it computes just a rough approximation of the real distances. Of course, the inaccuracy could be minimized by iteratively smoothing the paths but still, the result will be far from being optimal and the method slow as well.

Geodesic distance

Shortest path distance

To circumvent this problem, I tried another method. Instead of measuring the length of the shortest paths directly it relied on the fact that a real geodesic path unfolds into a straight line. So, what I basically did was:

• Compute the shortest path between point A and point B
• Unfold the path onto a plane
• Measure the Euclidian distance between point A and point B on the unfolded path.

Shortest paths

Unfolded shortest paths

Unfolded path (white), distance (red)

This method worked quite nicely but it has one big drawback – it doesn’t work on meshes with holes. As soon as the line drawn between the start- and endpoint of the unfolded path crosses a hole, the result is no longer the true geodesic distance.

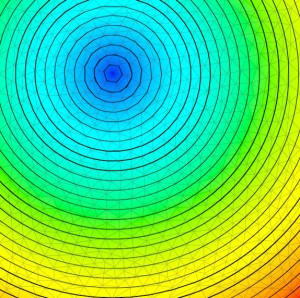
The third algorithm I´ve used was the well known Fast Marching Front Propagation Method. You start at the single source point and compute the distance to the 1-ring neighbouring points around it. By doing this iteratively and summing up the distances you´ll finally get the geodesic distance to all points in the mesh. This works because it is easy to calculate the distance to the third point of a triangle as soon as the other two distances are known.
For the first quick implementation i used python but it was way to slow to be usable. After replacing the slow list lookups in the code i got a 3 times speedup but it was still to slow which was the reason for porting the algorithm to the HDK. After that, it worked quite fast (around 270 times faster) but the general problem with this algorithm is, that it doesn´t work with obtuse triangles. In other words, it needs to work on a fairly clean and regular triangulated mesh. If this is not the case, you´ll end up with errors in the distance calculation which leads to larger errors and so forth. To prevent this from happening I had to insert conditional statements for obtuse triangles as well for all other special cases and hence the code got much longer and somewhat cluttered. Usually, when fast marching front propagation is used on 2D and 3D grids, this is not a problem but for arbitrarily triangulated meshes it is.

Finally I decided to implement the great paper: “Geodesics in Heat” by Keenan Crane. The method described in the paper works basically as follows:

• Integrate the heat flow for a source point across the mesh
• Compute the normalized gradient for the heat
• Solve the Poisson equation to get the actual distance

Integrate Heat

Compute gradient

Solve Poisson equation to finally get geodesic distance

One of the great advantages of the heat method is its brilliant simplicity. Basically it relies only on solving a sparse linear system what could be done quite efficiently by various linear algebra libraries (I’ve used Eigen for this). This makes it possible to compute the geodesic distances from more than one point in pretty much the same computation time, quite contrary to the marching method for example.

Geodesic distance from one point

Geodesic distances from four points

Geodesic distance from an edge

Back-tracing to compute the geodesic paths

Geodesic paths to different points

Mesh clipped at a specific geodesic distance

For some related reading:
K. Crane, C. Weischedel, M. Wardetzky: The Heat Method for Distance Computation
M. Novotni, R. Klein: Computing Geodesic Distances on Triangular Meshes
V. Surazhsky, T. Surazhsky, D. Kirsanov, S. J. Gortler, H. Hoppe: Fast Exact and Approximate Geodesics on Meshes
D. Bommes, L. Kobbelt: Accurate Computation of Geodesic Distance Fields for Polygonal Curves on Triangle Meshes