Computing curve skeletons of 3D shapes is an important tool in computer graphics with many different applications for shape analysis, shape matching, character skeleton construction, rigging and many more. It’s an active field of research and over the years, numerous algorithms have been developed. Most of these algorithms are based on mesh contraction using smoothing or thinning. Another popular approach is to use the voronoi diagram generated by the points of the mesh. Quite an interesting alternative, however, is to rely on spectral analysis for computing the skeleton. The idea is fairly simple and works as follows:
- Compute the first non-zero eigenvector of the Laplace-Beltrami operator, namely the Fiedler vector.
- Compute contour lines based on the Fiedler vector
- Find the center point for every contour
- Fit curves to the points

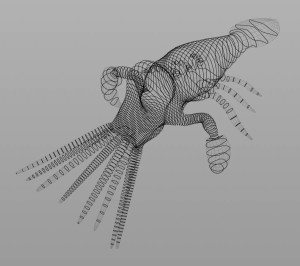

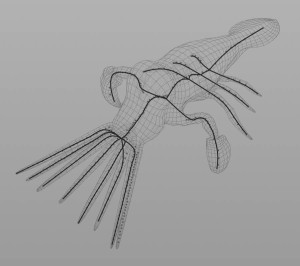
Wow, this is super useful!
May I have a file to study?
LikeLike
Unfortunately I can’t share the file but I’m always willing to help if you’re going for an implementation.
LikeLike
Could you elaborate on how you obtain the mesh contours from curve skeleton ?
LikeLike
Is it possible to generate the countour/isolines from Houdini’s built-in tools, or is that also custom-made? Thanks!
LikeLike
It’s just standard SOPs and a bunch of wrangles. I’ve attached an example file.
https://drive.google.com/open?id=0By9c7CX4X0HAaXZUS0JvQy1oN2
LikeLike
Ah, that’s very helpful, thank you!
LikeLike
Hello, could you please update the link ? It seems broken here.
LikeLike
I would love to see this amazing stuff as well, can you fix the link?
LikeLike
Amazing!
I have wanted to solve this problem for such a long time, of creating an automated “skeleton”, but never understood how to implement it.
“Compute the first non-zero eigenvector of the Laplace-Beltrami operator, namely the Fiedler vector”
Would you need special libraries for this step or is it possible to use houdini vex/volume combinations to create the Fiedler vector field?
As I understand Laplace-Beltrami operations is just computing the Laplacian of the geometry. Would it be possible to use the Laplacian field from the VDB analysis and later use it to get the first non-zero eigenvector ?
My math knowledge is limited, I have looked at the eigenvalues and eigenvectors, but I find it difficult to understand how to use them practically, on actual geometry.
Any help is greatly appreciated!
LikeLike
Sorry for the late reply, but I didn’t check the blog for a long time.
Well, in theory you could do the eigendecomposition with VEX and standard SOPs but it would be cumbersome and probably tremendously slow. However, you won’t need external libraries if you have access to the HDK.
Generally it’s not really common practice to use the Fiedler vector for skeleton extraction. It’s a nice idea but in practise this might lead to a number of problems because computing the Laplacian is very sensitive to irregular geometries. Most probably you might be better off by using a mesh contraction algorithm. This could be done directly on the mesh but it’s easier to use a VDB volume instead and simply relying on its gradient. I think there is a file somewhere on OdForce or the SideFx forum which is using this method.
Alternatively you could also search for the points at which the magnitude of the gradient vanishes instead of iteratively contracting the mesh. These points lie on the medial axis and could be used afterwards to compute the skeleton.
LikeLiked by 1 person
Hello!
i´m developing a sort of muscle simulation framework on houdini, and creating some little tools for each step of geometry preparation before simulation. I’m trying to figure out how to create an attribute on input muscles to automatically create a muscle fiber directions to use this attribute to drive anisotropic muscle contraction on FEM simulation. (right now i’m doing this manually, but i with to proceduralize this step too!)
i have some ideas, as use medial axis to detect volume “flow” of muscles, but i had no idea how to implement… searching on technical stuff i eventually found your blog! Can you help me on this?
thanks in advance.
you can see some result of R&D on my vimeo: https://vimeo.com/285373573
LikeLike
Hi, thanks for the blog, its a really great learning resource and exposes so many topics I never knew about.
I’ve attempted to solve the laplacian matrix’s eigenvectors via HDK (through python inlinecpp) with Eigen & Spectra external libraries. The laplacian matrix is just connectivity information with no weighting (not sure how much impact that has on solving).
I don’t know much about eigensolvers but I’m using a sparse symetric shift-and-invert method, this gives me the best results but is very sensitive to the shift value changing. One small change produces a completely different (and mostly incorrect) eigenvector.
Here’s a visualisation with an arbitrary shift value of 0.011
https://imgur.com/a/OXRavPz
Do you have any advice on what could produce a more stable result, is this solver mode suited for solving the smallest values of the laplacian? I can provide a cleaned up hip with the header libraries.
LikeLike